Lösung:

a) F(x): x .  ln(x²)
für x d.b für x ist immer R aller reale zahlen
jetzt für  ln(x²)  logarithmus ist nur für positive Zahlen also x²  > 0        also R äußer 0

Definitionsbereich also R außer { 0 }



Ableitung :

Wir benutzen die regel f'(x)= u . 'v.+ u . v'                                                        u'= 1
                                         =  1.  ln(x²)  +    x . 2/x                                        v'=  2x . 1/x² = 2/x
                                         =   In (x²) +2             also richtig !


Hochpunkt ---> Erste Ableitung gleich 0 setzen

0  =   In (x²) +2  | -2      ----- >     In (x²)= -2  |  /e      ---->  e^-2  =  x²      ----> x1 = 1/e   x2 = -1/e            2. Quadranten heißt hoch punkt in der negativen bereich also -x coordinate und überhalf der x - achse  ALSO x2 = -1/e   IST GEBRAUCHT


f''(x)= 2x . 1/x² = 2/x              jetzt x2 in f''(x)                   f''(-1/e)   < 0 also einen Maximum            damit wie diesem punkt finden. setzen wie die x2 in f(x)

f(-1/e  )= (-1/e )  .  ln((-1/e)  ²) = 2/e

P(-1/e | 2/e )



Zweite Aufgabe: Hilfsmittlefrei

geg f(x) = (2x-12) e^x und F(x) = (2x-14) e^x
a) Weisen Sie nach, dass F eine Stammfunktion von/ist.
b) Geben Sie die Gleichung F₂ einer weiteren, von F verschiedenen Stammfunktion von ƒ an.
c) Bestimmen Sie die Lösung der Gleichung   0∫tf (X) dx = 14


Lösung:

 a)  Muss     F'(x) = f(x)                             F'(x)= u . 'v.+ u . v'

   F'(x)= 2 . e^x  +   e^x . ( 2x - 14 )
       = e^x ( 2 + 2x - 14)
       = e^x (2x - 12)                                  dann F'(x) = f(x)


 b) ges: F2 (x)                      F2 (x) = F(x) + c                c= R                  einfach einen Wert für c nehmen                        z.b = 42 

        F2 (x)  =  e^x (2x - 12) + 42


 c)  0∫tf (X) dx = 14    gesucht ist t

                                                                                 t   
      0∫t (2x-12) e^x = 14        --->       (2x-14) e^x |                    Jetzt F(t) - F(0) Bilden.  ---->   e^t(2t-14)  -  e^0(2(0)-14) = e^t(2t-14) - 1(-14)
                                                                                      0                                                                                                        = e^t(2t-14) + 14


 Aber Wir wissen schon 0∫tf (X) dx = 14        also     e^t(2t-14) + 14 = 14
                                                                                 e^t(2t-14) = 0  

    Jetzt ist entweder e^t = 0 oder (2t-14) = 0
    und e^t ist niemals genau gleich null dann muss (2t-14) = 0        t = 7            Für t = 7  gilt 0∫tf (X) dx = 14




 Dritte Aufgabe : Integral Rechnung

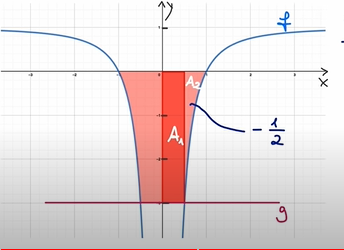
Gegeben ist die in R\{0} definierte Funktion f(x)=1 - 1/x^2 , die die Nullstellen x₁ = -1 und x₂=1 Die Abbildung zeigt den Graphen von f, der symmetrisch bezüglich der  y-Achse ist.                                                            
 Weiterhin ist die Gerade g mit der Gleichung y = -3 gegeben.

 a) Zeigen Sie, dass einer der Punkte, in denen g den Graphen von f schneidet, die x-Koordinate hat.

 b) Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von f, die x-Achse und die Gerade g einschließen


 Lösung:
 
  a)  Jetzt mussen wie zeigen dass die punkt s(0.5|?) die y coordinate -3 hat.     Wir konnen die 0.5 in die haupt funktion einsetzen und wenn -3 auskommt
  dann ist diesem punkt die schnittpunkt zwischen f(x) und y = -3 

  >f(0.5)=1 - 1/0.5^2 = -3            s(0.5|-3)  dann S ist die schnittpunkt mit dem coordinaten s(0.5|-3)

 b) Jetzt mussen wir die A berechnen.         A zwischen Y= -3 and f(x) und der X achse ist 
      
 Ages = 2(A1 + A2)

 A1 = lange . breite = 3 . 0.5 = 1.5 FE
                                                                           1                      1
 A2 =  0.5∫1 f(x)=1 - 1/x^2   dx = x - (-1).x^-1 |   = (x + 1/x) |     = 1 + 1 - (0,5 + 1/0,5) = -0,5 FE
      
                                                        0                  0
 > Ages = 2(1,5 + 0,5) = 4 FE